2024-2/Discreta/1.org

primera clase

• Intro
  • Parcial 1
• En el ultra
• Grafos
  • Bibliografia
  • Facts
• ej
  • 1
    • a
    • b
    • c
    • d
    • e
    • f
    • g
    • h
  • 2
  • 4
    • a
    • b
    • c
  • 6
    • 2-cubo
    • 3-cubo
  • doc bibliografia

Intro

Tenemos 2 parciales, 2 recuperatorio, 1 trabajo final y nota de concepto (no detona tu nota ni aprueba)👊. Se promociona con 8.

Parcial 1

Viene cargado. puede sacar temas.

En el ultra

Esta el programa, clase 1

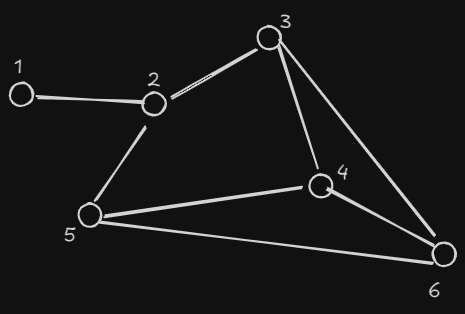
Grafos

Es una grafica de las relaciones entre nodos (ya sean personas,computadoras(da igual)).

Bibliografia

./matematicadiscreta.pdf

Facts

• Camino en un grafo es una sucesión de vértices del grafo tal que cada par de vértices consecutivos esté relacionado por una arista.
• En un grafo dirigido, un camino dirigido es una sucesión de vértices del grafo tal que para cada vértice de la sucesión (excepto el último) existe una arista dirigida desde ese vértice al siguiente en la sucesión.
• Dos vértices w y v están conectados si existe un camino w − v entre ellos.
• La longitud del camino (camino dirigido) es la cantidad de aristas que usa.
• Un recorrido es un camino que no repite aristas.
• Un circuito es un recorrido cerrado.
• Un camino simple es un camino que no repite vértices (excepto quizás el primero y el último en el caso de camino simple cerrado).
• Un ciclo es un camino simple cerrado.
• La distancia entre dos nodos w y v es la longitud del camino más corto entre w y v.

ej

1

a

Grafo	Cant
G1	3
G2	4
G3	4

b

• G1 f-f
• G2 g-g
• G2 h-h

c

Grafo
G1	a-b-c-d-a
G2	a-b-g-a
G3	-

d

Grafo
G1	a-b-c
G2	a-b-c
G3	a-b-c

e

Grafo
G1	-
G2	g-b-f-a
G3	-

f

grafo
G1	f-g
G2	d-f-c
G3	J

g

grafo
G1	g-e
G1	g-f-e
G2	g-a-f-d-e
G2	g-a-f-e
G2	g-a-f-b-c-d
G2	g-b-f-d-e
G2	g-b-f-e
G2	g-b-c-e
G2	g-b-a-f-d-e
G2	g-b-a-f-e
G3	g-i-j-e

h

grafo	Trasado	N
G1	b-a	1
	b-d	1
	b-c	1
G2	b-g	1
	b-a	1
	b-f	1
	b-c	2
	b-f-d	2
	b-c-e	1
G3	b-j	2
	b-j-f	2
	b-j-e	2
	b-j-i	2
	b-j-i-g	3
	b-j-i-k	3
	b-j-i-k-a	4
	b-j-i-k-a-h	5
	b-j-i-k-a-h-c	6
	b-j-i-k-a-h-d	6

2

4

a

• G4 Entrada = 3 Salida = 3
• G5 Entrada = 3 Salida = 3

b

grafo	Trasado
G4	e-c-b-a
G5	e-d-b-a

c

grafo	Trasado
G4	a-g-b-a
G5	-

6

2-cubo

U -- B
|    |
|    |
C -- V

U - B - V
U - C - V

3-cubo

doc bibliografia

./guia.docx

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
import numpy as np

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# Define vertices of the cube
vertices = np.array([[0, 0, 0], [1, 0, 0], [1, 1, 0], [0, 1, 0],
                     [0, 0, 1], [1, 0, 1], [1, 1, 1], [0, 1, 1]])

# Define the six faces of the cube
faces = [[vertices[j] for j in [0, 1, 2, 3]],
         [vertices[j] for j in [4, 5, 6, 7]],
         [vertices[j] for j in [0, 1, 5, 4]],
         [vertices[j] for j in [2, 3, 7, 6]],
         [vertices[j] for j in [0, 3, 7, 4]],
         [vertices[j] for j in [1, 2, 6, 5]]]

# Create a 3D polygon collection
poly3d = Poly3DCollection(faces, alpha=.25, linewidths=1, edgecolors='r')
ax.add_collection3d(poly3d)

# Set the limits and labels
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_xlim([0, 1])
ax.set_ylim([0, 1])
ax.set_zlim([0, 1])

plt.show()