3.4 KiB
title
| title |
|---|
| Resumen Parcial 2 Teoria |
Temas
- Cirtuito RC
- Capacitores
- Teoria de electromagnetismo
- Ejs de kircho(ff)
- convertir forma polar a rectangular
Clase 9 - Descripcion del capacitor
La capacidad es una relacion Q/V que establece la carga que contiene y la tension entre sus placas.
C = \frac{Q}{V}
V = \frac{Q}{C}
Q = C * V
Capacitor Placas Planas Paralelas
Consta de dos placas metálicas planas paralelas de área A, separadas una distancia d. Entre las placas se coloca un dieléctrico de permitividad \varepsilon . Resultando su capacidad:
C = \varepsilon \frac{A}{d}
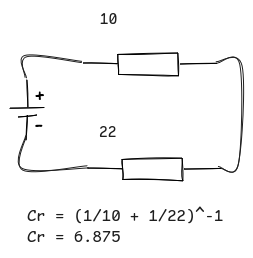
Medir Capacitores en Serie
tenemos que tener en cuenta que
\frac{1}{C_r} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + ...
{C_r} = ( \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + ... )^{-1}
Medir Capacitores En Paralelo
En este caso hay que sumar los dos capacitores porque actuan como un capacitor más grande
C_r = C_1 + C_2
Aplicaciones
Son utilizados como filtros para frecuencias y tambien para almacenar energia. Por ejemplo los flashes fotograficos lo utilizan.
tambien son utilizados en temporizadores y alarmas.
Pero un uso el cual estamos más en contacto todos los dias es el de las pantallas tactiles.
Cuentas
Capacitores en serie
si tenemos un circuito donde la fuente es de 120V y hay 3 capasitores en serie de:
- 4
\muf - 6
\muf - 2
\muf
Capacidad Equivalente
\frac{1}{C_e} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3}
\frac{1}{C_e} = \frac{1}{4} + \frac{1}{6} + \frac{1}{2}
C_e = 1.0909 \mu f
Luego hay que pasarlo a microfaradio a faradio por lo que pasaria a ser:
1.09*10^-6 F = 1.0909 \mu f
Carga total
q = \Delta V * C_e
q = 120V * 1.09*10^-6 F
q = 1.308^{-4} C
Energia del sistema
W = \frac{1}{2} * q * \Delta V
W = \frac{1}{2} * 1.308^{-4} * 120V
W = 7.848^{-3} J
Capacitores en Paralelo
si tenemos un circuito donde la fuente es de 120V y hay 3 capasitores en paralelo de:
- 4
\muf - 6
\muf - 2
\muf
Capacidad Equivalente
C_e = C_1 + C_2 + C_3
C_e = 4 + 6 + 2
C_e = 12 \mu f
C_e = 1.2*10^{-5}f
Carga total
q = \Delta V * C_e
q = 120V * 1.2*10^{-5}
q = 1.44*10^{-3} C
Energia en el sistema
W = \frac{1}{2} * q * \Delta V
W = \frac{1}{2} * 1.44*10^{-3} * 120V
W = 0.0864 J
Asociacion Mixta
Primero tenemos que hacer la relacion entre los capacitores que estan en serie. Vamos a empezar con el C_5 y C_6
C_{56} = (\frac{1}{12} + \frac{1}6{})^{-1} = 4 \mu f
Ahora sumamos con el del capacitor 4
C_{456} = C_4 + C_{56}
C_{456} = 4 \mu f + 4 \mu f = 8 \mu f
ahora con esto resueto podemos calcular todo en serie
C_{123456} = (\frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + \frac{1}{C_{456}})
C_{123456} = (\frac{1}{32} + \frac{1}{24} + \frac{1}{16} + \frac{1}{8})^{-1} = 3.84 \mu f = 3.84*10^{-6} F
Luego calculamos la carga total:
q = \Delta V * C_e
q = 120V * 3.84*10^{-6} F
q = 4.608*10^{-4}C
Luego calculamos las diferencias locales V1, V2 y V3
V1
V_1 = \frac{4.608*10^{-4}C}{3.2*10^{-5}}
V_1 = 14.4V
V2
V_2 = \frac{4.608*10^{-4}C}{2.4*10^{-5}}
V_2 = 19.2V
V3
V_3 = \frac{4.608*10^{-4}C}{1.6*10^{-5}}
V_3 = 28.8V
V_{456}
V_{465} = \frac{4.608*10^{-4}C}{8*10^{-6}}
V_{456} = 57.6V