2024-2/Discreta/entrega1.org

Trabajo Practico 1 - Matematicas Discretas

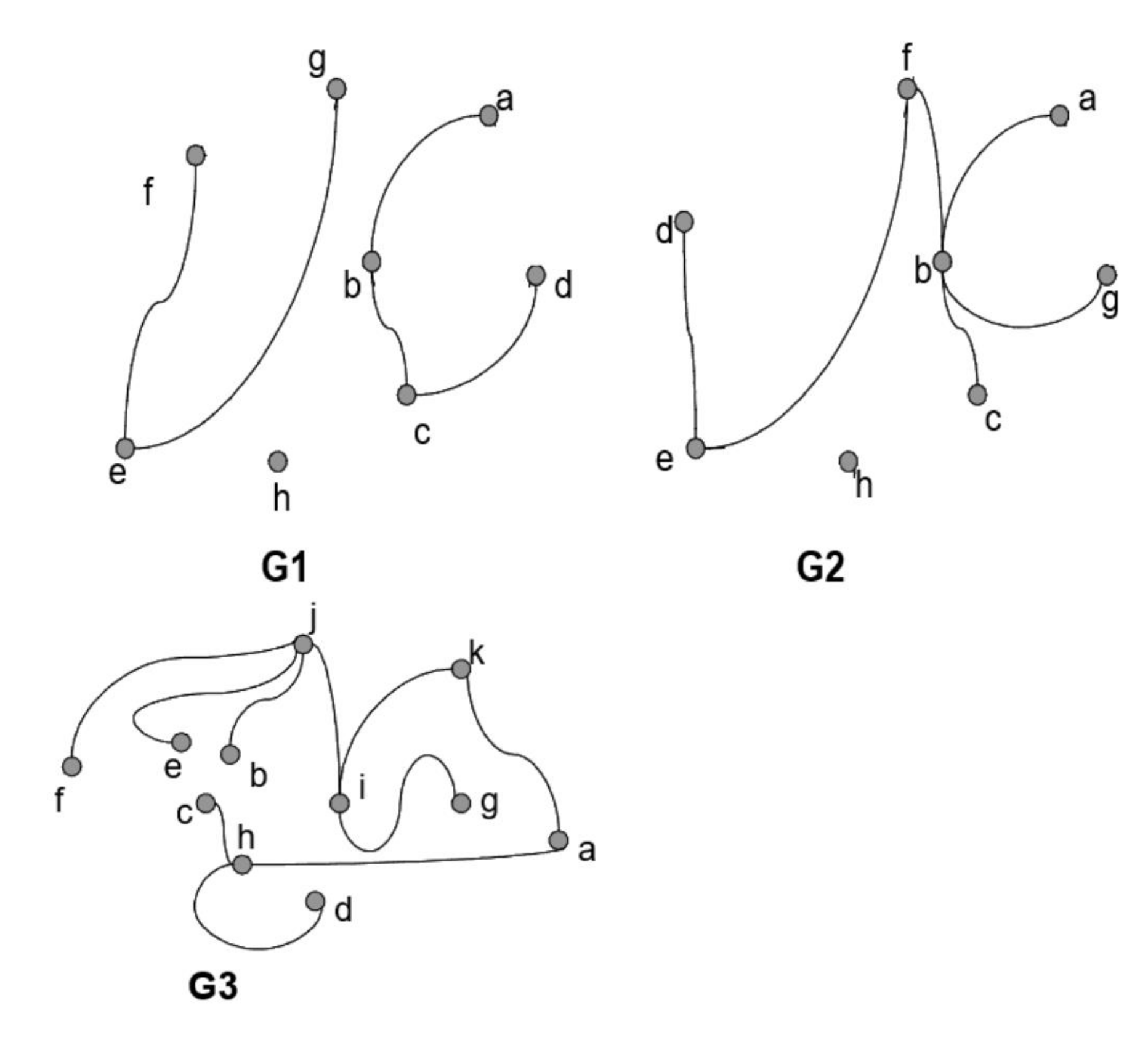
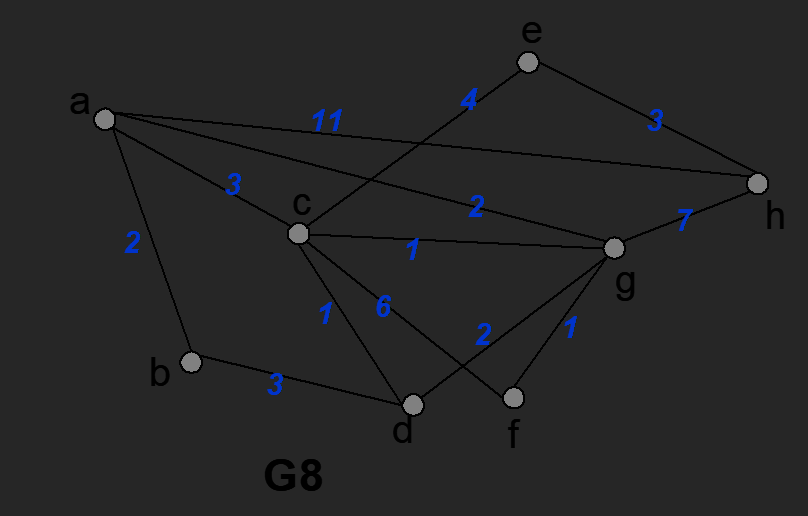
1 - Para cada uno de los grafos de la figura,

a. el grado de cada vértice. Verificar la fórmula que relaciona los grados de vértices con el número de aristas.

Grafo	Cant
G1	3
G2	4
G3	4

b. identificar los bucles (si existen)

• G1 f-f
• G2 g-g
• G2 h-h

c. un ciclo en el grafo

Grafo
G1	a-b-c-d-a
G2	a-b-g-a
G3	-

d. un camino de a a c de longitud 3, si existe

Grafo
G1	a-b-c
G2	a-b-c
G3	a-b-c

e. un ciclo que contenga a g, de longitud par, si existe.

Grafo
G1	-
G2	g-b-f-a
G3	-

f. los vértices conectados con e

grafo
G1	f-g
G2	d-f-c
G3	J

h. todos los caminos simples de e a g.

grafo
G1	g-e
G1	g-f-e
G2	g-a-f-d-e
G2	g-a-f-e
G2	g-a-f-b-c-d
G2	g-b-f-d-e
G2	g-b-f-e
G2	g-b-c-e
G2	g-b-a-f-d-e
G2	g-b-a-f-e
G3	g-i-j-e

i. la distancia entre b y cada uno de los vértices

grafo	Trasado	N
G1	b-a	1
	b-d	1
	b-c	1
G2	b-g	1
	b-a	1
	b-f	1
	b-c	2
	b-f-d	2
	b-c-e	1
G3	b-j	2
	b-j-f	2
	b-j-e	2
	b-j-i	2
	b-j-i-g	3
	b-j-i-k	3
	b-j-i-k-a	4
	b-j-i-k-a-h	5
	b-j-i-k-a-h-c	6
	b-j-i-k-a-h-d	6

2 - ¿Cuántas componentes conexas tienen los graos G1, G2 y G3? ¿Cuál es el número máximo de aristas que pueden eliminarse de cada uno, manteniendo el número de componentes conexas? ¿Cuál es el mínimo número de aristas que deben eliminarse para aumentar la cantidad de componentes conexas en cada grafo?

Grafo	N°Comp	Aristas Max	Aristas Min
G1	2	4	4
G2	2	5	3
G3	1	0	1

3

a. Escribir la matriz de incidencia de los grafos G1, G2 y G3.

• G1 \\

\begin{bmatrix} 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix}

• G2 \\

\begin{bmatrix} 0 & 1 & 0 & 0 & 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 1 & 0 & 0 \\ 1 & 1 & 0 & 1 & 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix}

• G3 \\

\setcounter{MaxMatrixCols}{12}

\begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ \end{bmatrix}

4 - Para los siguientes grafos dirigidos, indicar:

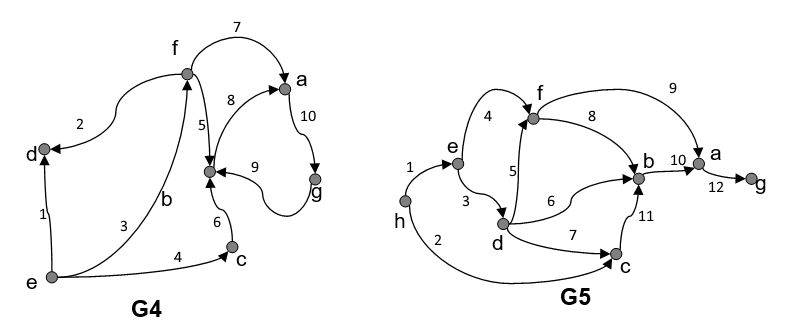
a. el grado de entrada y de salida de cada vértice. Verificar la fórmula que relaciona los grados de entrada y salida con el número de aristas.

• G4 Entrada = 3 Salida = 3
• G5 Entrada = 3 Salida = 3

b. un camino dirigido de e a a, si existe

grafo	Trasado
G4	e-c-b-a
G5	e-d-b-a

c. un ciclo dirigido, si existe

grafo	Trasado
G4	a-g-b-a
G5	-

5

a. Escribir la matriz de incidencia de los digrafos G4 y G5.

• G4\\

\begin{bmatrix} 0& 0& 0& 1& 1& 0& 0\\ 0& 0& 0& 1& 0& 1& 0\\ 0& 0& 0& 0& 1& 1& 0\\ 0& 0& 1& 0& 1& 0& 0\\ 0& 1& 0& 0& 0& 1& 0\\ 0& 1& 1& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 1& 0\\ 1& 1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 1\\ 1& 0& 0& 0& 0& 0& 1\\ \end{bmatrix}

• G5\\

\begin{bmatrix} 0& 0& 0& 0& 1& 0& 0& 1\\ 0& 0& 1& 0& 0& 0& 0& 1\\ 0& 0& 0& 1& 1& 0& 0& 0\\ 0& 0& 0& 0& 1& 1& 0& 0\\ 0& 0& 0& 1& 0& 1& 0& 0\\ 0& 1& 0& 1& 0& 0& 0& 0\\ 0& 0& 1& 1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 1& 0& 0\\ 1& 0& 0& 0& 0& 1& 0& 0\\ 1& 1& 0& 0& 0& 0& 0& 0\\ 0& 1& 1& 0& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0& 1& 0\\ \end{bmatrix}

b. Escribir la matriz de adyacencia de los digrafos G4 y G5.

Nota: La columna representa el destino y la fila el origen

• G4\\

\begin{bmatrix} 0& 0& 0& 0& 0& 0& 1\\ 1& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 1& 0& 1& 0\\ 1& 1& 0& 1& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0\\ \end{bmatrix}

• G5 \\

\begin{bmatrix} 0& 0& 0& 0& 0& 0& 1& 0\\ 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 1& 1& 0& 0& 1& 0& 0\\ 0& 0& 0& 1& 0& 1& 0& 0\\ 1& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 1& 0& 0& 0\\ \end{bmatrix}

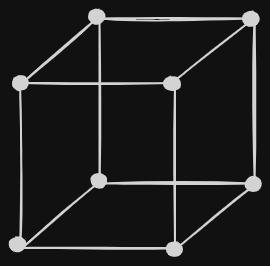
6 - Un n-cubo es un grafo en el que los vértices se etiquetan con n-uplas de ceros y unos. Una arista conecta dos vértices u y v si las etiquetas de u y v difieren exactamente en un símbolo.

a. 2-cubo

U -- B
|    |
|    |
C -- V

U - B - V
U - C - V

b. 3-cubo

c. ¿Es conexo el n-cubo? Justificar.

Es conexo porque existe un camino entre cualquier par de vertices.

d. Calcular el número de vértices y de aristas del n-cubo.

Para los vertices es:

\begin{center} 2^n \end{center}

y para las aristas

\begin{center} n * 2^{n-1} \end{center}

Entonces para un n-cubo siendo n = 3

\begin{center} $Vertices = 2^3 = 8$ $Aristas = 3 * 2^{3-1} = 12$ \end{center}

10 - Indicar si existe un grafo regular con las siguientes características (dar un ejemplo o justificar la no existencia):

Un grafo puede ser regular cuando se cumple que:\\

$\frac{2|\textit{E}|}{|\textit{V}|}= k$ donde $k\in\mathds{Z}$\\

Además, siempre y cuando $|\textit{V}|>1$, un grafo regular puede ser dibujado sin búcles.
Teniendo esto en cuenta:

a. 7 vértices y 7 aristas

$\frac{2\cdot{7}}{7}= 2$
2∈\mathds{Z}
El grafo puede ser regular.

b. 7 vértices y 16 aristas

$\frac{2\cdot{16}}{7}= 4,57$
4,57∉\mathds{Z}
El grafo no puede ser regular.

c. 3 vértices, 6 aristas, sin lazos

$\frac{2\cdot{6}}{3}= 4$
4∈\mathds{Z}
El grafo puede ser regular.

d. 4 vértices, 6 aristas, sin lazos

$\frac{2\cdot{6}}{4}= 3$
3∈\mathds{Z}
El grafo puede ser regular.

11 - Indicar para qué valores de n es regular:

Intervalos con números enteros

a. el grafo completo K_n

\begin{center} \left [ 3;\infty \right ) \end{center}

b. el ciclo de n vértices, C_n

\begin{center} \left [ 3;\infty \right ) \end{center}

c. la rueda de n+1 vértices, W_n

2

d. la estrella con n+1 vértices, S_n

1

e. el n-cubo

\begin{center} \left [ 1;\infty \right ) \end{center}

f. el grafo lineal L_n

1,2

12 - Hallar la matriz de adyacencia de los grafos: K_6 , C_6, W_5, S_5 , L_6.

K_6

\begin{bmatrix} 0 & 1 & 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 & 1 & 1 \\ 1 & 1 & 0 & 1 & 1 & 1 \\ 1 & 1 & 1 & 0 & 1 & 1 \\ 1 & 1 & 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 1 & 0 \\ \end{bmatrix}

C_6

\begin{bmatrix} 0 & 1 & 0 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 0 & 1 & 0 \\ \end{bmatrix}

W_5

\begin{bmatrix} 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 \\ \end{bmatrix}

S_5

\begin{bmatrix} 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ \end{bmatrix}

L_6

\begin{bmatrix} 0 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ \end{bmatrix}

14 - Dada la siguiente matriz de adyacencia de un grafo no dirigido

\setcounter{MaxMatrixCols}{12}

\begin{bmatrix} 0 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ \end{bmatrix}

Responder (sin graficar el grafo)

¿Cómo se puede determinar la cantidad de aristas en el grafo, a partir de dicha matriz?

Al ser una matriz de adyacencia simetrica el valor en una posicion (x,y) es igual al de una (y,x), vease con (1,5) y (5,1) donde el valor de ambos es 1 al representar la relacion entre el nodo 1 y el 5. Teniendo esto en cuenta lo que tendriamos que hacer es contar todos los 1's que hay en la matriz menos los que representan bucles en si mismos, vease (2,2) donde se representa un bucle, dividir esa suma por 2 y luego sumar los bucles por separado.

hay 15 aristas sin contar bucles y 18 aristas contando bucles.

Determinar el grado de cada vértice.

Como la matriz es no dirijida se cuenta cuantas aristas estan conectadas al mismo vertice.

• n°1 Vertice, Grado 4
• n°2 Vertice, Grado 1
• n°3 Vertice, Grado 4
• n°4 Vertice, Grado 2
• n°5 Vertice, Grado 3
• n°6 Vertice, Grado 2
• n°7 Vertice, Grado 4
• n°8 Vertice, Grado 4
• n°9 Vertice, Grado 3
• n°10 Vertice, Grado 2
• n°11 Vertice, Grado 2
• n°12 Vertice, Grado 2

Describir un algoritmo para determinar todos los vértices conectados con el primer vértice, teniendo como entrada la matriz de adyacencia, y aplicarlo a la matriz dada.

Se puede usar el algoritmo de busqueda de profundidad.

Tenemos 2 listas una de los vertices visitados y otra para el resultado. \\

• Empezamos con el vertice 1.
  Lo primero que hay que hacer es añadirlo a la lista de vertices visitados
  Luego lo añadimos a la lista de vertices resultado. Obtenemos una lista de todos los vertices a los que esta conectado: {3, 5, 7, 9}
  Vamos al 3
• Vertice 3
  Lo añadimos a la lista de vertices visitados {1, 3}
  Luego a la de resultado {1, 3} Obtenemos una lista de vertices a los que esta conectado: {1, 7, 9, 12}
  Vamos al 7
• Vertice 7
  Lo añadimos a la lista de vertices visitados {1, 3, 7}
  Luego a la de resultado {1, 3, 7} Obtenemos una lista de vertices a los que esta conectado: {1, 3, 5, 8}
  Vamos al 5
• Vertice 5
  Lo añadimos a la lista de vertices visitados {1, 3, 5, 7}
  Luego a la de resultado {1, 3, 7, 5} Obtenemos una lista de vertices a los que esta conectado: {1, 7, 8}
  Vamos al 8
• Vertice 8
  Lo añadimos a la lista de vertices visitados {1, 3, 5, 7, 8}
  Luego a la de resultado {1, 3, 7, 5, 8} Obtenemos una lista de vertices a los que esta conectado: {5, 7, 9, 11}
  Vamos al 9
• Vertice 9
  Lo añadimos a la lista de vertices visitados {1, 3, 5, 7, 8, 9}
  Luego a la de resultado {1, 3, 7, 5, 8, 9} Obtenemos una lista de vertices a los que esta conectado: {1, 3, 8}
  Finally!!!!

Entonces usando el algoritmo de profundidad solo se puede llegar hasta el 9 desde el primer vertice.

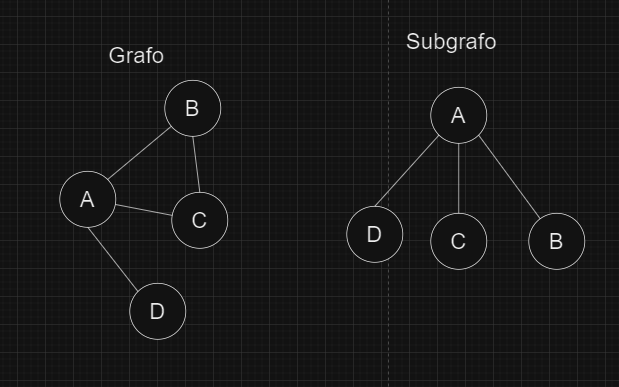
21 - ¿Cuál de los grafos G1, G2 o G3 es un árbol? Indicar los vértices colgantes (hojas).¿Cuántos caminos distintos hay entre cada par de vértices?

G3 es un árbol.
Las hojas son F, E, B, C, D, G
Existe un único camino entre cada par de vértices.

22 - Hallar árboles recubridores para cada una de las componentes conexas de los grafos del problema 1

23 - Hallar un árbol recubridor del grafo G6.

el arbol recubridor del grafo 6 seria

24 - Dibujar un grafo tal que admita un árbol recubridor con raíz de altura 1. Caracterizar los grafos tales que admitan un árbol recubridor de altura 1.

27 - Dada la siguiente matriz de pesos de un grafo

a. Dar un árbol recubridor minimal

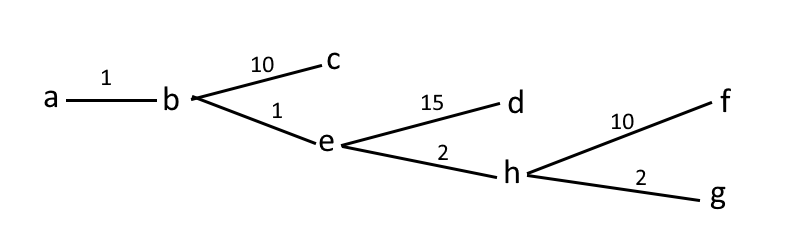
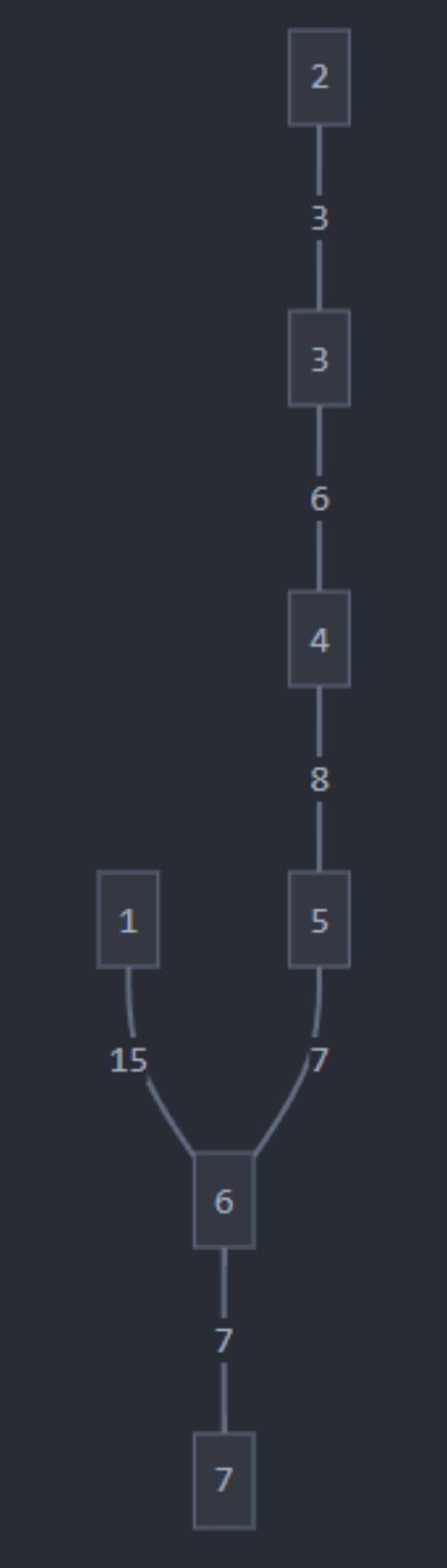
b. Considerando el árbol obtenido en el inciso anterior como un árbol con raíz en el vértice 1, ¿cuál es la altura?

Su altura es de 5

c. El grafo descrito por esa matriz, ¿admite un recorrido euleriano? Justificar.

No lo admite, existen más de dos vértices con grado impar (a, b, c, d…)

28 - Dada la siguiente matriz de pesos de un grafo, dar un árbol recubridor minimal, e indicar su peso.

D=

\begin{bmatrix} 1 & 17 & 18 & 17 & 16 & 15 & 20 \\ 17 & 2 & 3 & 0 & 0 & 0 & 0 \\ 18 & 3 & 1 & 6 & 0 & 0 & 0 \\ 17 & 0 & 6 & 0 & 8 & 0 & 0 \\ 16 & 0 & 0 & 8 & 20 & 7 & 0 \\ 15 & 0 & 0 & 0 & 7 & 0 & 7 \\ 20 & 0 & 0 & 0 & 0 & 7 & 1 \\ \end{bmatrix}

el peso es de 46.

30 - Las conexiones entre las terminales de una red de 6 equipos se muestran en el grafo G8. También se indican los tiempos de transmisión de un mensaje de un equipo a otro. Hallar el camino por el que el equipo a debe transmitir un mensaje al equipo h en menor tiempo.